今天是數學課，要來說說時間複雜度跟漸進式符號

什麼是時間複雜度？

為什麼要討論時間複雜度？

我們前面介紹了演算法的 5 大標準。
那要怎麼評斷哪個演算法是比較好的呢？
先來定義甚麼叫做「好」：通常來說，在可以達成相同結果的情況下，效率較佳的程式是比較好的。
因此，我們要用時間複雜度的概念，來評估演算法的效率。

而某個程式的 Time Complexity = 部署時間 + 執行時間

通常部署時間是與電腦效能有關，所以我們基本上會討論「執行時間」
那執行時間要怎麼得知呢？有兩種方式：

1. 直接測量實際時間：但這又跟電腦的效能有關係了，所以基本上不採用
2. 預估分析：分析指令的執行次數來評估演算法的效率，基本上都是採用這個方式。

求指令執行次數：

以下有個程式：

int function(int n){
    int a;
    a = 3;
    for(int i = 1; i < n; i++){
        a = (a + i) * 2;
    }
    return a;
}

這個程式總共執行了：
賦值給變數：1次 + for 迴圈判斷式：n 次 + for 迴圈內指令：n - 1 次 + return 敘述：1次 = 2n + 1 次

可能有人會問了，又不是每個指令的執行時間都一樣
沒錯，所以有另一種計算的方式就是把每個指令依照時間加權，然後算出執行次數
但一般來說，我們都會將每個指令的執行時間及難易程度視為相同

那什麼是漸進式符號

看看下面兩個程式

int function(int n){
    int a = n + 3;
    n = a;
    return n;
}

int function(int n){
    return n + 3;
}

上面兩個程式碼做的事情相同，但上面的花了 4 個指令完成，下面的只花了 2 個指令。
其實這兩個執行時間沒差多少，就因為 code style 的關係，我們因此要說上面的程式比下面的差嗎？
顯然並不是很公平，因此在數學上，有個符號來消除這種不平等，也就是漸進式符號（Asymptotic Notation）
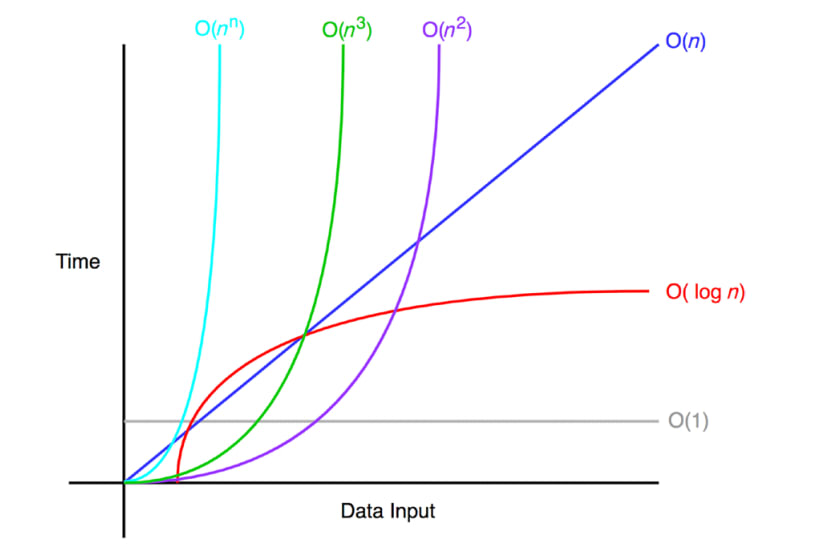
我們不用指令的執行次數來評估，而是使用程式隨著輸入的資料量的增加之成長速率來評估

漸進式符號的種類：

我們介紹 3 種最常見的：

1. Big-Oh: O
   定義：若且唯若 f(n) = O(g(n))，則存在兩個正常數 c、n0，使得0 <= f(n) <= c * g(n)，對所有的n >= n0皆成立
2. Big-Omega: Ω
   定義：若且唯若 f(n) = Ω(g(n))，則存在兩個正常數 c、n0，使得0 <= c * g(n) <= f(n)，對所有的n >= n0皆成立
3. Theta: θ
   定義：若且唯若 f(n) = θ(g(n))，則存在三個正常數 c1、c2、n0，使得0 <= c1 * g(n) <= f(n) <= c2 * g(n)，對所有的n >= n0皆成立

如果看完定義已經傻了，那就來練習一題：
Q: f(n) = 4n + 9 則 O(?)？
Ans: 令g(n) = n，取 c = 5，n0 = 9，使得 0 <= 4n + 9 <= 5n，對所有的n >= 9皆成立，因此f(n) = O(g(n))

漸進式符號的意義

從定義來看，g(n) 就是一個界線，無論 f(n) 如何成長，最終只可能趨近於 g(n)，而不會超過 g(n)
因此：

1. big-oh 表示：就算程式在最壞情況，程式的執行時間（f(n)）也不會突破 g(n) 這個函數，因此代表了執行時間的上界（upper bound）
2. big-omega 表示：就算程式在最佳情況，程式的執行時間（f(n)）也不會低於 g(n) 這個函數，因此代表了執行時間的下界（lower bound）
3. theta 表示：無論程式在何種情況，程式的執行時間（f(n)）也不會偏離 g(n) 這個函數，因此代表了執行時間的緊界（tight bound）

常見的成長速率等級

1. O(1)：常數時間。如：Stack 的 pop 和 push
2. O(logn)：對數時間。如：Heap 的 insert 和 delete
3. O(n)：線性時間。如：Binary Search Tree 的 traversal algorithm
4. O(n * logn)：介於線性時間與平方時間之間。如：Quick Sort, Merge Sort 的 Average Time
5. O(n^2)：平方時間。如：Bubble Sort, Selection Sort
6. O(2^n)：指數時間。如：Tower of Hanoi
   
   這些在接下來的文章中都會一一提到喔！以後也都會用漸進式符號來分析演算法的成長速率等級！
   再複習最後一次：漸進式符號代表的就是：隨著輸入量的增加，演算法的成長速率等級！

結束數學課啦，明天要進入第一個大主題了：Stack

參考網址：https://thedukh.com/2020/10/what-is-the-logarithmic-runtime-ologn/